MG
[ML / Andrew Ng] Linear Regression - Model and Cost Function 본문
[ML / Andrew Ng] Linear Regression - Model and Cost Function
MG# 2022. 4. 28. 15:21
이번 파트에서는 머신러닝을 위한 모델을 설명합니다. 이전 단원에서 설명했던 Regression 문제에서 집의 크기가 x, Input이 되고 집의 가격이 y, Output 그리고 그 훈련 데이터의 개수를 m 이라고 합니다. (x, y) 를 하나의 훈련 세트라고 합니다. 그리고 그 순서에 따라 (x^i, y^i) 로 나타냅니다.

그리고 이를 예측하기 위한 가설(Hypothesis)함수가 존재합니다. 이 단원에서는 변수가 하나인 선형 회귀로 나타내었습니다. 이 함수를 이용해 x값을 토대로 y값을 산출해 냅니다.

h 함수(가설 함수)를 보다 정확하게 맞추기 위해 비용함수(Cost Function)이 필요합니다. J 함수로 표시하고 h 함수의 값과 실제 결과값인 y와 비교를 해 오차의 제곱을 모든 훈련 데이터셋 m 세트 다 더합니다. 그래서 h 함수의 목표는 J 함수의 최솟값을 찾는 것입니다. 그러면 Input 값이 들어올때 비교적 정확히 Output 을 예측할 수 있기 때문입니다.

간단하게 하기 위해 h(x) = (theta)x 로 정의하고 J 함수를 그립니다. 그러면 theta 의 값에 따라 우측 그래프처럼 J 함수의 값이 변하게 됩니다. 여기서 h 함수의 기울기인 theta 를 변하게 하다보면 theta 가 1에서 J 함수가 최소가 되는 것을 확인할 수 있습니다. 위 그림에서와 같이 오차가 0이 되고 모든 데이터셋과 h 함수가 일치하는 것을 확인할 수 있습니다.
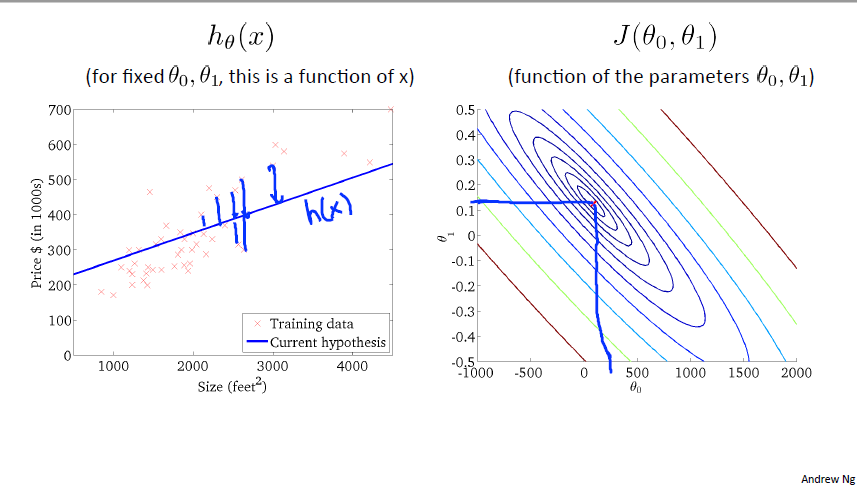
h 함수를 원래대로 theta_0, 1로 이루어진 함수로 정의하면 J 함수도 그에 따라 변하는 것을 볼 수 있습니다. J 함수는 현재 등고선 형태로 나타내었고 색깔이 같은 지점은 J 함수의 값이 모두 같다고 표시한 것입니다. 이를 토대로 theta_0, 1 값을 조정하다 보면 J 함수의 가운데 지점에서 최솟값이 되고 좌측 그림에서 데이터셋 위로 h 함수가 지나가는 것을 확인할 수 있습니다.
'컴퓨터과학 > AI_ML강의 (Andrew Ng)' 카테고리의 다른 글
| [ML / Andrew Ng] Linear Regression - Computing Parameters Analytically (Normal Equation) (0) | 2022.05.02 |
|---|---|
| [ML / Andrew Ng] Linear Regression - Multivariate Linear Regression (0) | 2022.05.02 |
| [ML / Andrew Ng] Linear Regression - Parameter Learning (Gradient descent) (0) | 2022.04.28 |
| [ML / Andrew Ng] Introduction (0) | 2022.04.28 |
| ML 강의 (Andrew Ng) 시작 (0) | 2022.04.24 |




