[ML / Andrew Ng] Linear Regression - Multivariate Linear Regression

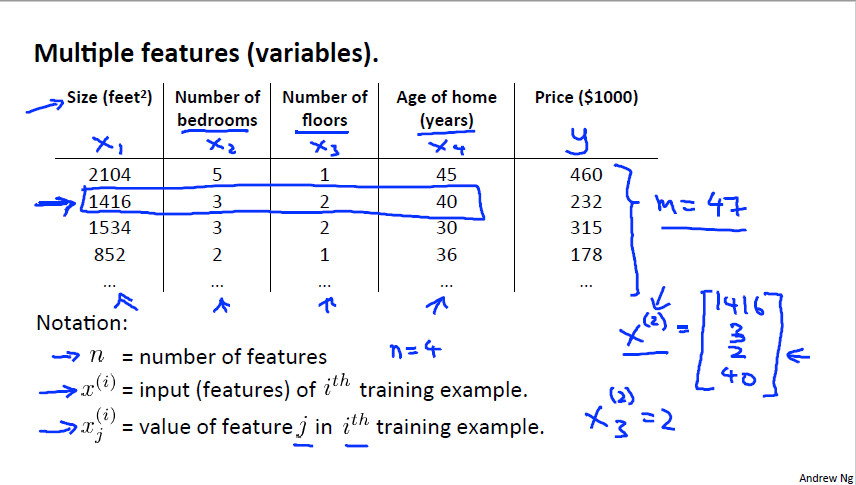
이전 강의에서는 특징(변수)가 1개인 Univariate Regression 만 다루었습니다. 하지만 현실에선 2개, 3개 또는 거의 무한한 변수가 존재하게 됩니다. 이를 Multivariate Regression 이라고 합니다. m 개의 training sets 에서 각 set 당 n 개의 변수가 주어집니다. 여기서 x 는 변수이고 i번째 set 의 j번째 변수로 정의합니다.

Multivariate Regression 에 Gradient Descent 를 적용시켜보면 위 그림과 같이 됩니다. 원래 사용했던대로 식을 사용하지만 이전과는 다르게 x가 n + 1 차원을 가지고 있기에 theta 도 마찬가지입니다. 그렇기에 이를 모두 계산해주는 것만 다릅니다. 오른쪽 아래 그림에서 미분도 똑같이 진행되는 모습을 확인할 수 있습니다.

이제 저희가 Gradient Descent를 직접 적용시킬때 x값을 보정하는 방법 2가지에 대해 알아봅시다. 첫번째로 Feature Scaling 입니다. 말 그대로 feature인 x의 크기를 조정하는 것인데 x값을 x의 범위로 나누면 됩니다. 그 나누는 값은 x의 최댓값에서 최솟값을 뺀 값 또는 표준편차로 나누어줍니다.

 

이를 사용하는 이유는 Feature Scaling을 적용하지 않았을때인 그림인 왼쪽과 적용한 오른쪽 그림을 비교해보면 알 수 있습니다. 보다시피 x1과 x2는 크기부터 이미 꽤 차이가 납니다. 이렇게 되면 J함수의 그래프가 뾰족한 타원모양을 그리게 되고 이 그래프에 Gradient Descent를 적용시키면 Convergence하는 과정에서 불필요한 움직임이 생기게 되고 결과적으로 시간이 더 오래걸리게 됩니다. 하지만 이 방법을 적용시키면 오른쪽 그림과 같이 완만한 타원을 그리게 되어 시간이 더 절약됩니다. 그래서 Feature Scaling을 사용하면 효율적으로 계산이 가능합니다.

2번째 방법은 Mean Normalization입니다. 이 방법은 x값을 그 값들의 평균으로 빼준 후 계산하는 방법입니다. 그 이유는 하나의 변수의 평균이 극단적으로 차이가 나 어느 한 곳에 몰려있을 수 있기 때문에 그래프를 0 주변으로 모으기 위함입니다.

 

위에 나왔던 Feature Scaling과 이 방법을 같이 사용하게 되면 평균 크기와 위치 둘 다 보정이 되기에 변수가 -0.5 ~ 0.5 사이에 있는 등 특정 위치에 모여있기에 분석하고 시각화하는데 용이합니다. 그렇기에 보통 같이 사용하는 모습을 확인할 수 있습니다. (이는 고등학교 통계에서 배우는 정규분포 등으로 배우는 그 내용입니다.)

다음은 Learning rate에 대해 다뤄보겠습니다. 이전 강의에서 alpha(= learning rate)를 적당한 값으로 정하지 않으면 너무 느리게 convergence하거나 overshooting하는 문제점을 확인하였습니다. 그래서 이 값을 어떻게 하면 적절히 정할 수 있을까 입니다.

 

이에 앞서 위 그림을 보면 x축에는 반복횟수, y축에는 J함수의 값을 그린 그래프가 주어지고 A, B, C 중 올바른 alpha값을매치해보는 문제입니다. 여기서 앞서 말한 문제점이 바로 보입니다. B는 반복횟수에 따른 J값 갱신이 느리기에 0.01, C에서는 J값이 아예 증가해버리는 overshooting이기에 0.1 그리고 A가 적당한 0.1이라고 추정해볼 수 있습니다. 저희는 이 적당한 값을 추정해야 합니다.

정답은 그냥 대입해보는 것입니다. alpha값을 0.001로 설정하고 결과가 이상하면 10배 증가한 0.01, 0.1 ... 등으로 갱신하면서 그래프를 그려보는 것입니다. Andrew 교수님은 실제로 이 방법을 적용할 때 더 구체적인 값을 찾기 위해 3배씩 alpha값을 증가한다고 하였습니다. 이렇게 적당한 alpha값을 구할 수 있습니다.

마지막으로 Polynomial Regression에 대해 알아보겠습니다. 앞에서는 완전히 다른 변수들로 이루어진 Regression이었지만 똑같은 변수를 제곱하거나 루트를 씌우는 방법으로 변수를 증가시킬 수 있습니다. 이를 적용하는 이유는 그림과 같이 2차함수를 그리게 되면 극대값 이후에선 size가 증가하지만 역설적이게 y값이 감소하는 가격이 오히려 줄어버리는 이상한 현상이 생기게 됩니다. 이를 방지하기 위해 3차함수 또는 루트를 씌운 함수를 만들게 됩니다.

 

결국 똑같은 x를 가지고 계산을 하지만 x1, x2 ... 으로 여러 변수가 생긴 것처럼 보입니다. 이렇게 더 정확한 예측을 위해 하나의 변수를 늘릴 수 있다는 것도 알아보았습니다.