[ML / Andrew Ng] Logistic Regression - Classification and Representation

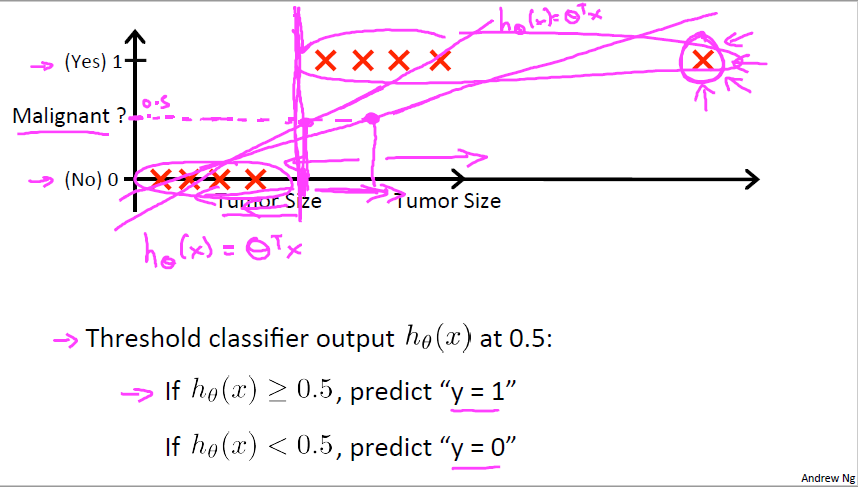
앞서 설명했었던 Supervised Learning의 한 종류인 Classification을 다시 다룹니다. 우리가 지금까지 Linear Regression을 이용하여 예측을 했기에 이를 그대로 적용하면 될 것 같지만 문제가 생깁니다. 위 그림은 종양의 크기를 알았을 때 악성인지 양성인지 추측하는 문제입니다. 위와 같이 데이터가 모여있고 오른쪽에 위치한 데이터처럼 동떨어진 데이터가 생길 경우 당연히 우린 악성 종양이라고 판단하지만 Linear Regression은 저 데이터 하나 때문에 이 전의 데이터들의 판단을 수정하게 되어 정확도가 떨어진 함수가 됩니다.

 

이 이유는 오른쪽 데이터를 넣기 전까지는 함수가 합리적으로 예측했지만 오른쪽 데이터를 추가하는 순간 그래프가 오른쪽으로 더 기울어 져버리기 때문에 앞의 데이터를 틀리게 판단해버리기 때문입니다. 결과적으로 우리 눈으로 봐도 간단한 Classification 문제를 컴퓨터가 못 푸는 상황이 나와버립니다. 이를 해결하기 위해 우리는 다른 함수를 가져와야만 합니다.

그렇게 등장한 새 방법이 바로 Logisic Regression 입니다. 우리는 Classification 문제를 해결하기 위해 새로운 h함수를 정의하는데 이 함수를 Logistic function 또는 Sigmoid function 이라고 부릅니다. 모양만 봐도 Linear function 과는 완전히 달라진 것을 확인할 수 있습니다.

h함수를 정의하자면 theta 로 표현가능한 x가 주어졌을때 y = 1인 것을 정확히 예측할 확률입니다. 함수로는 h(x) = P(y = 1| x;theta)로 표현됩니다. 그러므로 h함수는 결국 확률함수 입니다. 그렇기에 h 함수에 x가 주어졌을때 y= 1 일 확률과 y = 0 일 확률을 더하면 100퍼센트이기에 1이 되는 성질을 갖고 있습니다.

 

Classification 문제는 앞 강의에서 봤던 Regression 예시들처럼 가격을 맞추는 문제 등의 연속적인 값을 예측하는게 아닌 말 그대로 분류를 하기에 0 또는 1일 확률을 예측할 수밖에 없는 것입니다. 그래서 Logistic Regression 은 h 함수가 과반수인 0.5 를 넘었을때 그 결과일 확률만 말해줍니다. 암 진단을 받은 환자에게 우리는 70%로 암에 걸릴 것입니다 라고 말하지 0.7 악성 종양을 갖고 있고 0.3 양성 종양을 가지고 있다고 말할 수 없기 때문입니다.

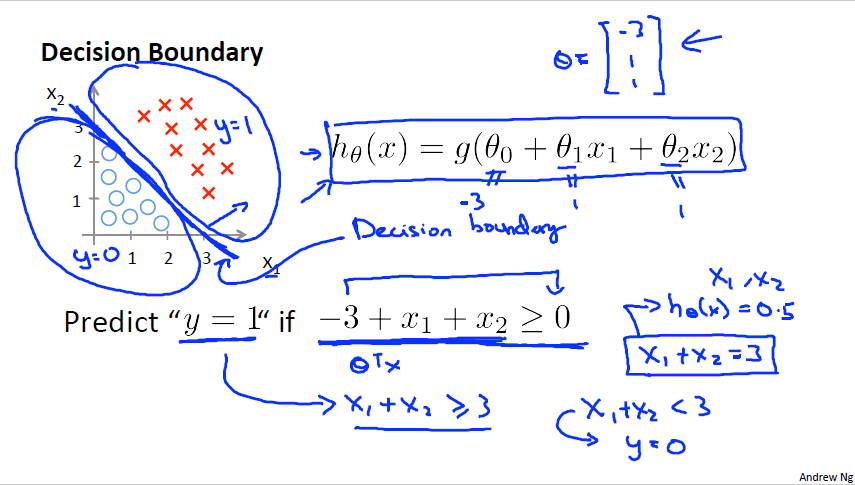
Decision Boundary는 Classification의 핵심인 분류에 대해서 설명합니다. 한국어로 직역해 보자면 결정경계 입니다. 말 그대로 h 함수를 그리고 그 경계를 중심으로 결과가 나뉘어지기 때문입니다. 위 그림에서 보듯이 h함수 밑으로 O, 위로는 X 표시로 나뉘는 것을 확인할 수 있습니다. 위 예시에 적용해 보자면 h함수가 0.5 이상인 구간에서는 악성, 이하인 구간에서는 양성으로 나뉘기에 0.5가 Decision Boundary 라고 할 수 있습니다.

앞선 예시는 Linear한 경계였다면 Non-linear decision boundary도 존재합니다. 이 경계를 파악할 때는 h함수를 0 보다 큰지 작은지로 구분합니다. 위 두 그림에서는 0보다 크면 y = 1, 작으면 y = 0으로 예측하였다. 이 경계는 함수에서 보듯 theta가 고정되는 순간 경계도 고정이 되기에 theta에 의존합니다.